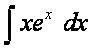Question Answer - 1

Soalan daripada kawan saya:

Solution:

Question (a)
We know that total number of students is 35 but n(A∪B∪C) ≠ 35.

There are three students who did not choose any subject. 
So, we have n(A∪B∪C)' = 3. Then

n(A∪B∪C) = 35-3 =32

From the first three rows, we know that 

n(A) = 17, n(B) = 15 and n(C) = 21

The forth, fifth and sixth rows have word "and" which means "intersection" represents by this symbol ∩. From the information, we know that

n(A∩B) = 10, n(B∩C) = 11 and n(A∩C) = 9

Question (b)

Number of students who chose all three subjects = n(A∩B∩C). 

n(A∪B∪C) = n(A) + n(B) + n(C) - n(A∩B) - n(B∩C)
                       - n(A∩C) + n(A∩B∩C)
aaaaaaaa32 = 17 + 15 + 21- 9 - 11 - 10 + n(A∩B∩C)
n(A∩B∩C) = 9

There are nine students who chose all three subjects.

Question (c)
No. of students chose who Anthropology only 

= n(A) - n(A∩B) - n(A∩C) 
   + n(A∩B∩C)

= 17 - 9 - 10 + 9

= 7

Question (d)

No. of students who have two favorite subjects 

= [n(A∩B) - n(A∩B∩C)] 
     + [n(B∩C) - n(A∩B∩C)] 
     + [n(A∩C) - n(A∩B∩C)]
= (10 - 9) + (11 - 9) + (9 - 9)
= 1 + 2 + 0 
= 3

Integration Strategy

Let’s get on with the strategy.

1. Simplify the integrand, if possible

Many integrals can be taken from impossible or very difficult to very easy with a little simplification or manipulation. Don't forger basic trigonometric and algebraic identities as these can often be used to simplify the integral. For example consider the following integral; 

2. See if a simple substitution will work

Look to see if a simple substitution can be used instead of the often more complicated methods. For example consider both if the following integrals.

The first integral can be done with partial fractions and the second could be done with a trig substitution. However, both could also be evaluated using the substitution .

and the work involved in the substitution would be significantly less than the work involved in either partial fractions or trigonometric substitution. 

So, always look for quick, simple substitutions before moving on to the more complicated techniques.

3. Identify the form of integral

If steps 1 and 2 have not led to the solution, then we take a look at the form of the integrand f(x).

Trigonometric functions

f (x)  is a product of sinx and cosx, tanx and secx, or cotx and cscx 
[use trigonometric methods]

Rational functions

f (x)  is P(x) divided by D(x) 
[use partial fractions]

LPET 

f (x)  is a product of polynomial, trigonometric function, exponential, or logarithm [use integration by parts]

f (x)  involve 
[use trigonometric substitutions]

Quadratic form 
[completing the square on the quadratic]

4. Try again

If the first 3 steps have not produced the answer, remember that there are basically only 2 methods of integration : substitution and by parts.

a) Try substitution

Even if no substitution is obvious, some inspiration or ingenuity may suggest an appropriate substitution.

b) Try by parts

Although integration by parts is used most of the time on LPET, it is sometimes effective on single functions. 

For examples:


c) Manipulate the integrand

Algebraic manipulations (rationalizing the denominator/ using trigo identities) may be useful in transforming the integral into an easier form. For examples:

d) Relate the integral to an integral that we already know how to do.
When you have build up some experience in integration, you may be able to use a method on a given integral that is similar to a method you have already used on a previous integral. Or you may be able to express the given integral in terms of a previous one. 

For example:
 

and if  
has previously been evaluated, then that calculation can be used in the present problem.


e) Use several methods.
Sometimes 2 or 3 methods are required to evaluate an integral. The evaluation could involve several successive substitutions of different types, or it might combine integration by parts with one or more substitutions.

Jom Bermain dengan Nombor

Anda cuma bermain dengan nombor apabila anda menjawab soalan matematik.

Hai semua!

LPET

If the integrand f (x) is a product of polynomial, trigonometric function, exponential or logarithmic, then integration by parts may work.

Key concept:

The challenge is to choose u and dv. Choose u and dv in such a way that:

u is easy to differentiate

dv easy to integrate

Remember this term LPET
L - ln
P - polynomial
E - exponential
T - trigonometric

How to use LPET?

Choose u for the first term of LPET and dv for the second term of LPET.

Example:

f (x) is a product of polynomial and trigonometric. 
From LPET,  we have PE. 
Then, u = polynomial and dv = trigonometric

More examples:

Second example, f (x) is a product of exponential and trigonometric. 

From LPET,  we have ET. 
Then, u = exponential and dv = trigonometric


Third example, f (x) is a product of polynomial and ln. 

From LPET,  we have LP. 
Then, u = ln and dv = polynomial

We Use Statistics Everyday

Do you realize that we live in a statistical world everyday?

Let's go through an example.

The definition of statistics: Science of collecting, organizing, analyzing, and interpreting data.