If the integrand f (x) is a product of polynomial, trigonometric function, exponential or logarithmic, then integration by parts may work.
Key concept:
The challenge is to choose u and dv. Choose u and dv in such a way that:
u is easy to differentiate
dv easy to integrate
Remember this term LPET
L - ln
P - polynomial
E - exponential
T - trigonometric
How to use LPET?
Choose u for the first term of LPET and dv for the second term of LPET.
Example:
f (x) is a product of polynomial and trigonometric.
From LPET, we have PE.
Then, u = polynomial and dv = trigonometric
More examples:
Second example, f (x) is a product of exponential and trigonometric.
From LPET, we have ET.
Then, u = exponential and dv = trigonometric
Third example, f (x) is a product of polynomial and ln.
From LPET, we have LP.
Then, u = ln and dv = polynomial


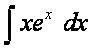







2 comments:
what if the the equation with different integrand, but in a division form.
example) ∫ (cos x) / (5x^3)
Great and that i have a dandy provide: modern kitchen remodel
Post a Comment